مسابقاتِ کشتی را تماشا کردهاید؟ در مسابقات کشتی هیچگاه یک فرد با وزن ۹۰ کیلوگرم را با فردی با وزن ۱۲۰ کیلوگرم رو در رو نمیکنند. در واقع هر شخص باید در محدودهی وزنِ خود کشتی بگیرد. در دادهها نیز شما نمیتوانید یک مجموعهی داده که مثلاً در بازهی بین ۰ تا ۲۰ متغیر هستند را با مجموعهی دادهای که در بازهی بین ۰ تا ۱۰۰۰۰ قرار دارد، مقایسه کنید. در واقع این دو مجموعهی داده بایستی ابتدا هم وزن شوند تا تاثیرِ یکی بیشتر از دیگر نباشد و به اصطلاح fair و منصف باشند.
اگر با درسِ ابعاد و ویژگیها آشنایی داشته باشید احتمالاً شکل زیر برای شما قابل فهم است. فرض کنید میخواهید مشتریانِ خود را بر اساس ۲ ویژگیْ خوشهبندی کنید (یعنی به دو گروهِ مختلف تقسیم کنید). ویژگیِ اول، سنِ افراد (محور عمودی) و ویژگیِ دوم، حقوقِ ماهیانهی افراد (محور افقی) است:
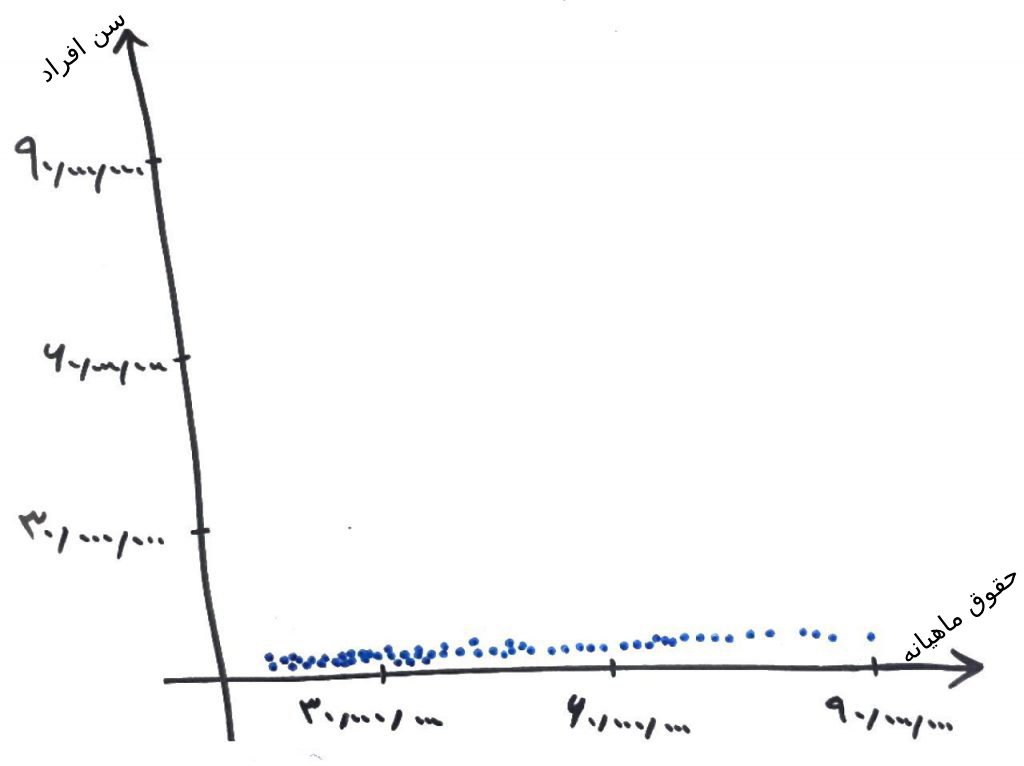
همانطور که مشاهده میکنید، دادهها در ۲ بُعد گسترش یافتهاند. بُعدِ اول (محور عمودی)، سن که معمولاً بین ۲۰ تا ۹۰ سال است و بُعدِ دوم (محور افقی) حقوقِ ماهیانه که معمولاً بین ۹،۰۰۰،۰۰۰ تا ۱۰۰،۰۰۰،۰۰۰ ریال متغیر است. حال اگر بخواهیم با استفاده از الگوریتمهای خوشهبندی، عملیاتِ خوشهبندی را بر روی این دادهها انجام دهیم، ویژگیِ حقوقِ ماهیانه (محورِ افقی)، تاثیر بسیار زیادی بر روی الگوریتم میگذارد (به خاطر اینکه بازهی بزرگتری از اعداد را در بر میگیرد و در اصطلاح scale بیشتری دارد). یعنی تقریباً ویژگیِ سن، تاثیری بر روی الگوریتم ندارد. این یکی از مواقعی است که دادهها در بازهی تغییراتِ متفاوت میتوانند تاثیر غیرِ دلخواهی بر روی همدیگر و به تبعِ آن بر روی الگوریتم، قرار دهند. پس دادهها باید در یک بازهی (range) مساوی نسبت به یکدیگر قرار بگیرند، مثلاً همه در یک بازهای مانند ۰ تا ۱ قرار داشته باشند و به این کار نرمالسازی دادهها یا data Nnormalization گفته میشود.
روشهای مختلفی جهتِ نرمالسازی دادهها وجود دارند که سعی داریم در دورهای جدا در مورد هر کدام به تفکیک صحبت کنیم. اما در این درس به یکی از معروفترینِ این روشها خواهیم پرداخت که به MinMaxNormalization معروف است. در این روش هر کدام از دادهها را میتوان به یک بازهی دلخواه تبدیل کرد. فرمول کلی MinMaxNormalization برای تبدیل دادهها به بازهی بین ۰ تا ۱ به صورت زیر است:
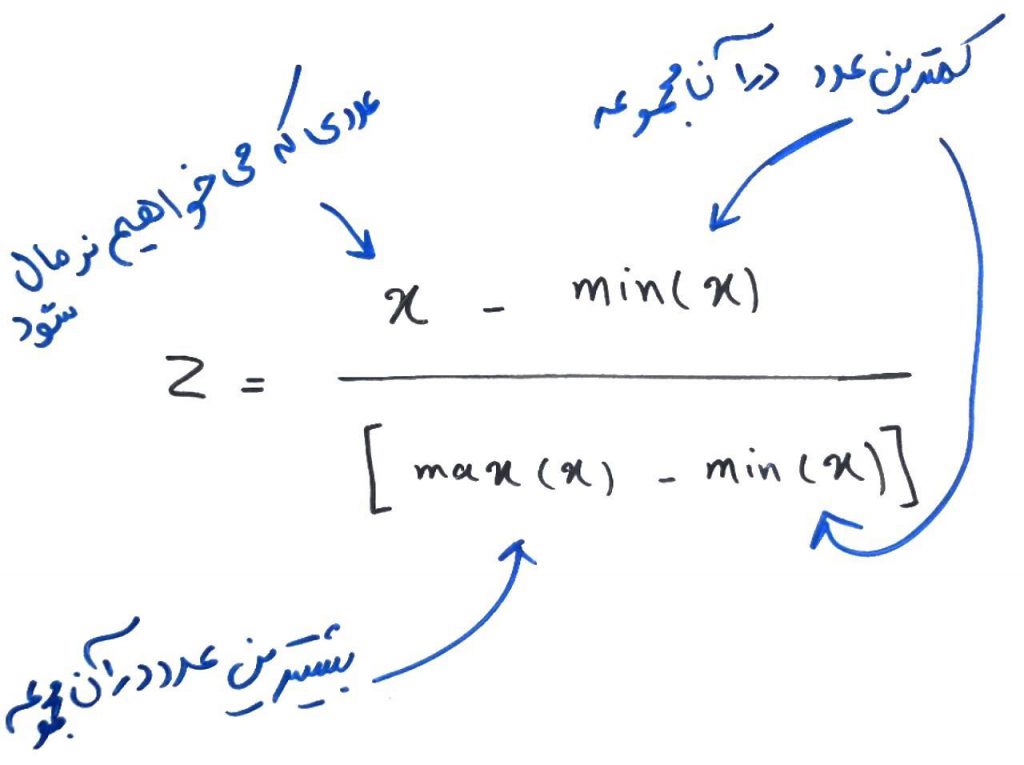
برای مثال فرض کنید دادههای سن برای افراد مختلف مانند شکل زیر است و ما میخواهیم سنِ این افراد را در یک بازهی ۰ تا ۱ قرار دهیم. با توجه به فرمول بالا نتیجه به این صورت است:
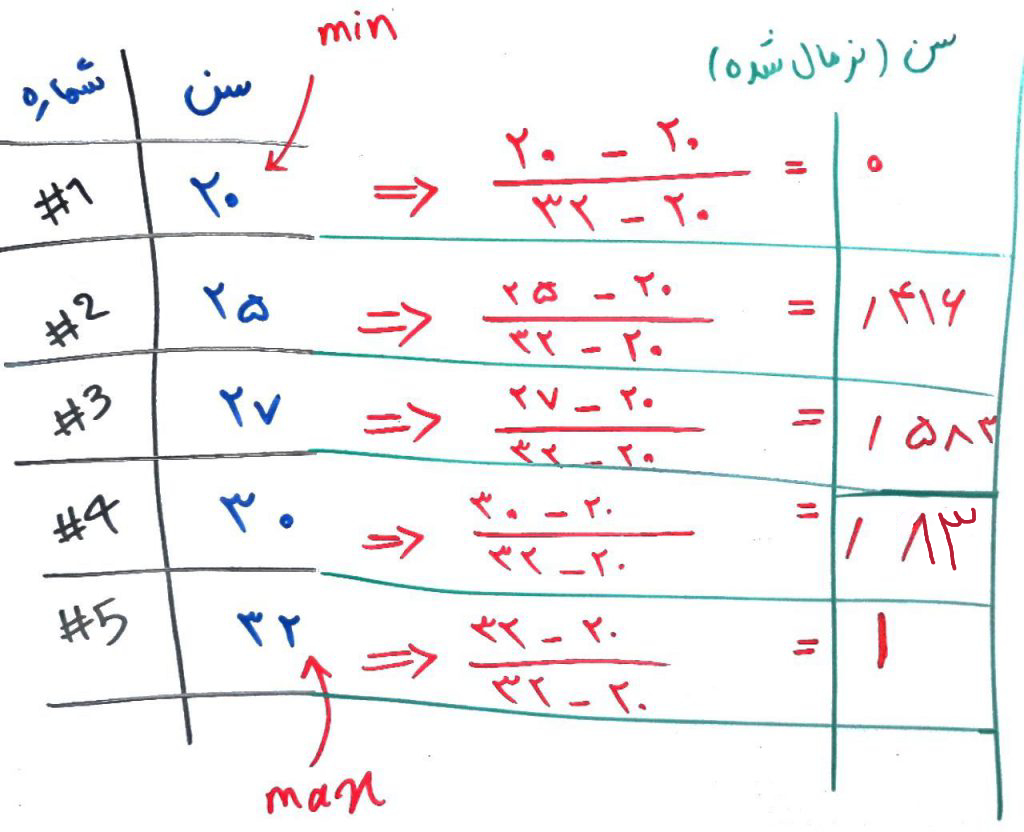
همانطور که میبینید هر کدام از نمونهها با توجه به مقادیرِ کمینه (min) و بیشینه (max) به بازهی ۰ تا ۱ تبدیل شدهاند. همین کار را میتوان برای ستونهای دیگر مانند حقوق انجام داد. شکل اولِ این درس را ببینید. با نرمالسازیِ دادهها در بازهی ۰ تا ۱، نمودار در ۲ بُعدی چیزی شبیه به شکل زیر میشود:
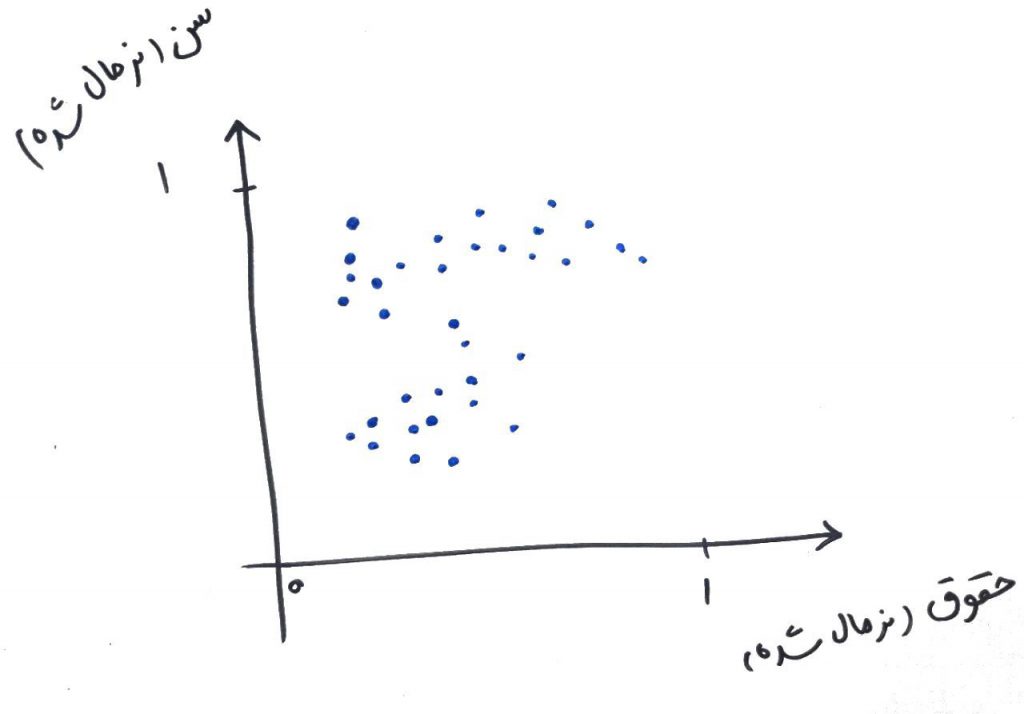
یعنی مقیاسِ هر دو ویژگی در بازهی ۰ تا ۱ قرار گرفته و حالا میتوان الگوریتمهای مختلف خوشهبندی و یا طبقهبندی را بر روی آنها به صورت منصفانه اجرا کرد.
عملیات نرمالسازی قبل از بسیاری از الگوریتمهای دادهکاوی مانند شبکههای عصبی، SVM، KNN و KMeans بایستی انجام بگیرد تا ابعادِ مختلف به صورت عادلانه توسط الگوریتم بررسی شوند و تاثیرِ یکی بیشتر از بقیه نباشد.
